Digitaalielektroniikka
Digitaalielektroniikka|
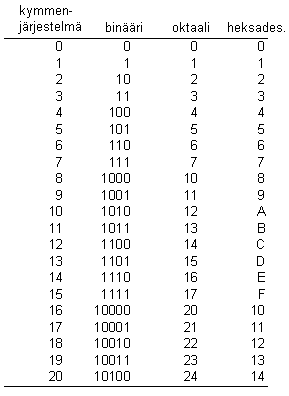
Bitti, sana ja tavu Yhdellä yksittäisellä loogisella arvolla eli bitillä (bit) ei voida esittää kuin hyvin pieni määrä informaatiota (on tai ei, esimerkiksi yö tai päivä). Jos halutaan esittää enemmän informaatiota, käytetään useamman bitin ryhmiä eli digitaalisia sanoja (word). Usealla bitillä voidaan esimerkiksi ilmaista kellonaika. Se kuinka tarkasti kellonaika ilmaistaan riippuu bittien määrästä. Sanan pituus, eli kuinka monesta yksittäisestä bitistä sana koostuu, vaihtelee tapaus- ja sovelluskohtaisesti. Tyypillisesti sanan pituus on esim. 8-, 12-, 16-, 24-, 32-, 64- tai 128-bittiä. Yksi digitaalitekniikan alkuajoista käyttöön jäänyt termi on tavu (byte, B), joka tarkoittaa kahdeksan bitin ryhmää. Esimerkiksi kaikki tietokoneisiin liittyvät muistituotteet ilmoitetaan tavujen avulla (..., kB, MB, GB,...), vaikka käytännössä nykyisin tietokoneiden käsittelemät sanapituudet ovat esim 32 ja 64 bittisiä, ja yhden sanan esittämiseen menee useampi tavu. Lisäksi täytyy muistaa, että usein digitaalimaailmassa esim. kilo tarkoittaa 1024=210 (ei kuitenkaan aina). Tavu ja bitti menevät maallikolla käsitteinä helposti sekaisin, ja tämä näkyy mm. mainoksissa, joissa esimerkisi digikameran muistimäärien, pikseleiden ja värisyvyyksien ilmoituksissa saattaa esiintyy kaikenlaista kummaa. Digitaaliset lukujärjestelmät Digitaalinen sana voi sisältää erilaista informaatiota, se voi esimerkiksi tarkoittaa lukuarvoa tai alfanumeerista merkkiä. Ihmisen käsitellessä numeroarvoja käytössä on kymmenjärjestelmä, joka periytyy ammoisilta ajoilta, jolloin huomattiin käsissämme olevan kymmenen sormea. Kymmenjärjestelmässä käytössämme on kymmenen symbolia (0, 1, 2,...9), joilla kaikki lukuarvot voidaan esittää. Järjestelmä on myös järjestyksestä riippuva, siis esimerkiksi luvussa 3254 numero 3 on eniten merkitsevä ja 4 vähiten merkitsevä luku. Yksittäinen bitti voi saada vain kaksi arvoa. Yhdistelemällä yksittäisiä bittejä tavuiksi ja sanoiksi on mahdollista esittää suurempia lukuja. Kaksikantaisessa lukujärjestelmässä esitettävien eri arvojen määrä saadaan laskettua seuraavan periaatteen mukaan: N kappaleella bittejä voidaan esittää 2N erilaista lukua. Esimerkiksi jos käytössämme on neljä bittiä (24 = 16), näillä voidaan esittää esimerkiksi kymmenjärjestelmän luvut välillä 0-15, kts. seuraava taulukko. Jos tässä esimerkissä haluttaisiin esittää myös negatiiviset lukuarvot, tarvittaisiin vielä yksi bitti kertomaan luvun etumerkki. Esimerkki tarvittavien bittien määrästä vuorokauden aikojen esittämissä. Luonnollisestikaan 2-kantajärjestelmä ei ole ainoa digitaalitekniikassa käytettävä lukujärjestelmä. Oheisessa taulukossa on esitelty muutama esimerkki, jossa desimaali- ja binäärilukujärjestelmän lisäksi on esitetty oktaali ja heksadesimaalilukujärjejestelmiä.
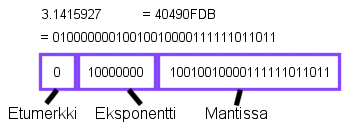
Negatiivisten numeroiden, desimaalilukujen, potenssien ym. esittämiseksi tarvitaan muita keinoja. Esimerkiksi nk. liukuluvuilla (floating point number) pystytään esittämään kokonaislukujen lisäksi hyvinkin tarkasti hyvinkin suuria ja pieniä lukuja, joilla on desimaaliosa. Seuraavassa esimerkkikuvassa on 32-bittinen liukuluku, jonka esitysmuodossa ensimmäinen bitti kertoo luvun etumerkin, seuraavat 8 bittiä muodostavat eksponentin ja viimeiset 23 bittiä nk. mantissan. Lyhyesti selitettynä luvun mantissa kertoo luvun varsinaiset merkitsevät numerot ja eksponetti skaalaa luvun suuruusluokan. Tästä ja muista digitaalisista numerojärjestelmistä lisää muilla kursseilla.
|