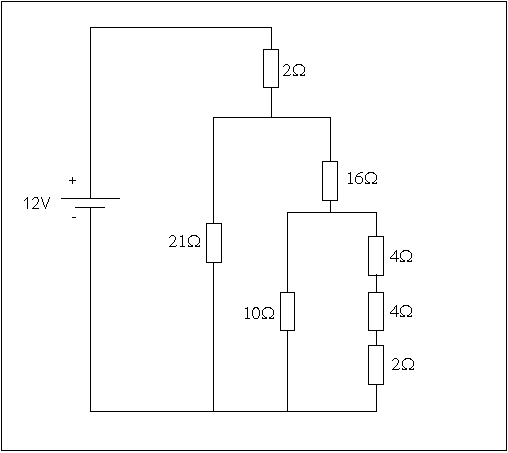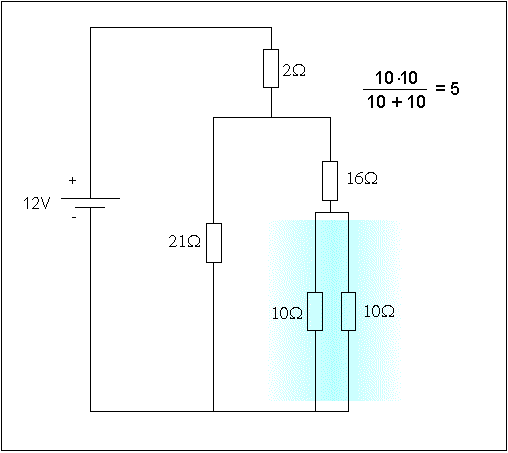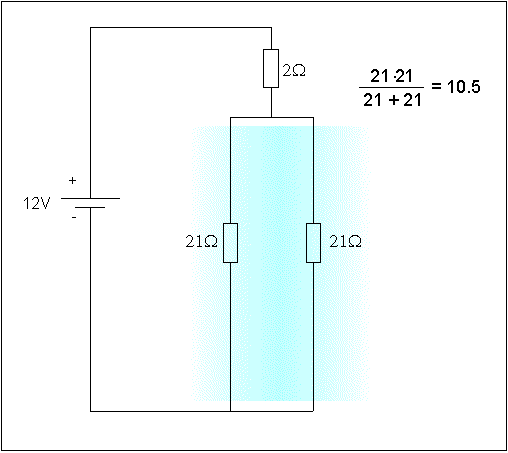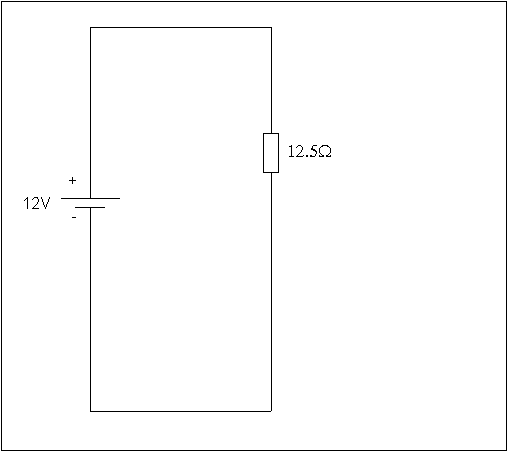
Esimerkki: Vastuskytkentöjen sieventäminen ja yksinkertaistaminen
 

Tarkastellaan kuvan mukaista kytkentää. Laske kytkennän ottama teho ja virta, jos piiri kytketään 12V ideaaliseen akkuun.

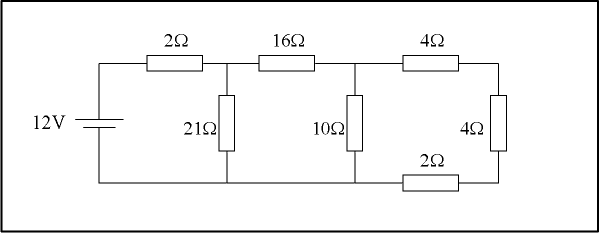
Ratkaisuesimerkki:

Usein hahmottamista auttaa kytkennän piirtäminen uuteen järjestykseen, jolloin kytkentää on helpompi lohkoa pieniin palasiin. Tämän jälkeen kannattaa vastusten ryhmä korvata yhdellä vastuksella, joka vastaa arvoltaan koko kytkennän vastusarvoa (katsottuna 12 V:n akun liitynnästä).

Lähdetään sieventämään kytkentää seuraavasti:

  1. Summataan ensin äärimmäisenä oikealla olevat vastukset. Koska vastukset ovat sarjaan kytkettyjä, kokonaisvastus on yksittäisten vastusarvojen summa: 4Ohm + 4Ohm + 2Ohm = 10Ohm.
  2. Lasketaan rinnakkain kytketyt vastukset, eli edellä laskettu 10Ohm vastus ja tämän vierelle oleva 10Ohm:n vastus. Rinnan kytketyille vastuksille saadaan (10Ohm*10Ohm)/ (10Ohm + 10Ohm) = 5 Ohm.
    Koska rinnakkain kytketyt vastukset ovat tässä esimerkissä yhtä suuret, saadaan vastaus myös suoraan muistisäännöstä: Kahden rinnakkain kytketyn samansuuruisen vastuksen aiheuttama kokonaisvastus on puolet yhden vastuksen arvosta.
  3. Summataan seuraavaksi sarjaan kytketyt vastukset 5Ohm + 16Ohm = 21Ohm.
  4. Lasketaan rinnakkain kytkettyjen vastusten 21Ohm ja 21Ohm kokonaisvastus (jälleen yhtäsuuret). Saadaan 10.5Ohm.
  5. Lopuksi summataan vielä sarjaan kytketyt vastukset 10.5Ohm ja 2Ohm, josta saamme koko piirin kokonaisvastuksen eli 12.5Ohm.

Piirin kokonaisresistanssiksi saatiin siis 12.5Ohm. Tämä vastaa koko vastushässäkän kokonaisresistanssia jännitelähteen liittimistä tarkasteltuna. Jännitelähteen kannalta koko kytkentä voidaan siis korvata yhdellä 12.5Ohm:n vastuksella. 

Tämän perusteella voidaan laskea akusta otettava virta, joka on Ohmin lain mukaan:

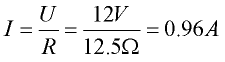I=U/R=0,96 A.

Akusta otettava teho (vastuksissa lämmöksi muuttuva teho) saadaan tehon kaavasta:

P=UI

 

Takasin kappaleeseen
© Mikko Kuisma, Satu Leinonen