Vahvistin

Esimerkki vahvistuksen laskemisesta

Laske jännitevahvistukset A_u = U_o / U_i, A_us = u_o / u_s , sekä virta- ja tehovahvistukset seuraavasta vahvistimesta. Vahvistimen jännitevahvistus on A_{uo =} 1000. (kuvassa varsinainen katkoviivoitettu vahvistinmalli on jännitevahvistimeksi mallinnettu):

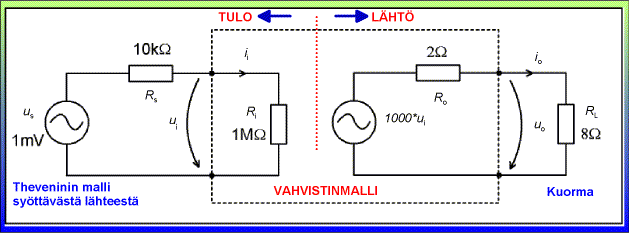
Vahvistimen tuloon vahvistettavaksi menevä jännite u_isaadaan laskemalla tulovirta i_i ja käyttämällä Ohmin lakia (u_i= R_i* i_i). Tulovirta on lähdejännite u_s jaettuna tulopiirin kokonaisvastuksella R_s + R_i ( i_i = u_s/(R_s + R_i) = 1 mV/(1010000 ohm) = n. 990 pA). Sievennettynä ilman välivaiheita saadaan edellinen tarina muotoon:

= n. 0,990 mV

Huomaamme, että kaikkea syöttävän lähteen signaalista (1 mV) ei saadakkaan vahvistimen tuloon asti, vaan osa signaalista häviää matkalla. Tässä häviötä tapahtuu syöttävän lähteen lähtöresistanssissa R_s, johon syntyy jännitehäviö u_R_s = i_i*Rs .

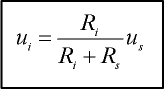<>Koska tehtävänannossa kuormittamattoman vahvistimen jännittevahvistus A_uo = 1000, saadaan vahvistimen sisälle olevaan (kuvitteelliseen, mallinnettuun) jännittelähteeseen generoitua jännite A_uou_i= 1000*u_i= n. 0,990 V

u_o saadaan ratkaistua tämän perusteella samalla tavoin kuin u_i yllä, sillä piirihän on samanlainen, kuin edellä laskettu (kaksi vastusta ja jännitelähde). Vahvistimen lähtöjännitteeksi (eli kuorman päiden väliltä mitattavaksi jännitteeksi) saadaan

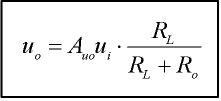= n. 0,792 V

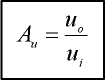Nyt voimme laskea koko vahvistinkytkennän jännitevahvistuksen A_u, kun mukaan tarkasteluun otetaan syöttävä piiri resistansseineen sekä vahvistimen perään kytketty kuormitus:

= n. 800

Tämä kuvaa piirin käytännön vahvistusta piirin tulosta lähtöön. Huomaa, että käytännössä saavutettu vahvistus on nyt pienempi, kuin vahvistimen sisäinen vahvistus ( tehtävässä 1000).

Seuraavaksi laskemme vielä vahvistuksen syöttävästä lähteestä kuormitukselle, eli A_us on

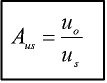= n. 792

Ja tämähän on vielä edellistäkin pienempi.

Teoriaosassa esitettyjen yhtälöiden nojalla saadaan virtavahvistukseksi

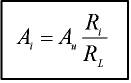= n. 100 000 000 = 1*10⁸(= n. 160dB)

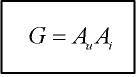Vastaavasti kytkennän tehovahvistus on

= n. 80 000 000 000 = 8*10¹⁰(= n. 109dB)