20µF kondensaattori on kytketty vaihtojännittelähteeseen E, jonka jännite on muotoa u(t)=50sin(200t).

Kappaleessa esitetystä impedanssin yhtälöstä voidaan ratkaista aluksi kondensaattorin impedanssi kytkennässä käytetyllä taajuudella 200 rad/s (= n. 31.8 Hz). Muokkamalla kaavaa vielä hieman (siellä kaavassa oli se ikävä j ja tulos on kompleksinen), saadaan impedanssin itseisarvo :

|Z|= 1/(200*20E-6)= 250

Tämän perusteella voidaan laskea kyseisessä kytkennäsää kulkeva virta Ohmin lain avulla. Esimerkiksi huippuvirta saadaan

Ipeak= 50V/250 =0.2 A

Vastaavasti muita suureita voitaisiin laskea ohmin lain avulla.

Huom ! Jos kytkennässä olisi muita komponentteja, tulisi kondenssaattorin impedanssin yhtälössä esiintyvä kompleksinen osa ottaa huomioon, koska virta ja jännite ovat vaihesiirrossa. Tällöin voitaisiin käyttää apuna esimerkiksi osoitinlaskennan keinoja (Sähköiset piirit -kurssilla lisää asiaa kiinnostuneille)

Seuraavissa kuvissa on esitetty kondensaattorin jännite, virta, teho ja energia yhden jakson ajalta.

Kondensaattorin jännite (= syöttöjännite) vaihtelee sinimuotoisesti.

Kondensaattoriin kytketyn jännitteen käyrämuoto vaihtelee sinimuotoisesti.

Kondensaattorin virta vaihtelee myös sinimuotoisesti, mutta on -90° vaihesiirrossa.

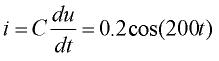
Kondensaattorin virran käyrämuoto vaihtelee myös sinimuotoisesti, mutta on eri vaiheessa jännitteeseen nähden.

Kondensaattorin teho voidaan laskea tehon kaavasta p = ui. Teho on negatiivinen kun kondensaattorin varausta puretaan. Seuraavaa kuvaa tarkastellessa havaitaan, että kondensaattoria varataan osassa jaksoa, ja puretaan toisessa osassa jaksoa. Varaukset ovat samansuuruisia kummallakin puolijaksolla, joten keskimäärin teho on 0. Huomaa, että teho vaihtelee kaksinkertaisella taajuudella jännitteeseen tai virtaan nähden. Tätä voidaan selittää vaikka edellisen kaavan perusteella siten, että teho p on 0 jännitteen u tai virran i ollessa 0 (kts. ylempiä kuvia).

Kondensaattorin teho ajan funktiona. Keskimäärin teho on esimerkissämme 0, koska teho vaihtelee ajan kuluessa samanasuuruisena sekä negatiivisella että positiivisella puolella. 

Kondensaattoriin varastoitunut energia voidaan laskea

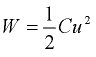
Kuvassa tämä näkyy siten, että kondensaattoriin varattaan tietyssä jakson osassa energiaa, ja toisessa jakson osassa energia puretaan pois. Esimerkissä energia koko ajan positiivinen. Ideaalista kondensaattoria voi käyttää häviöttömänä energiavarastona, käytännössä osa energiasta häviää kondensaattorin sisäisiin epäideaalisuuksiin, ja muuttuu esim. lämmöksi.

Esimerkkimme kondensaattorin energia ajan funktiona.

Kaikki samassa kuvassa:

.