Ratkaise piirissä kulkeva virta I ja vastusten yli olevat jännitteet, kun vastukset R = 10 ja R_s = 0,15 ja lähdejännite E = 3,0 V.

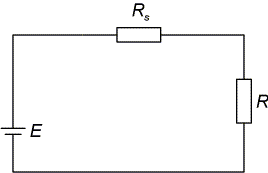
Ratkaisu

Kirchoff 1:

Koska virtapiiri ei haaraudu, kulkee koko piirissä sama virta I.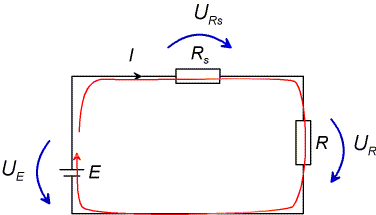

Kirchoff 2:

Koko piirin yhteenlaskettu jännite on nolla.

 Toisin muotoiltuna lähdejännite U_E on saman suuruinen, kuin vastuksissa R_s  ja R tapahtuva jännitehäviö. Vastuksissa oleva jännitehäviö voidaan taas laskea Ohmin lain avulla kun vastus ja virta tiedetään. Täälöin saadaan:

 U_E = R_sI + RI = (R_s + R)I

Virta I voidaan ratkaista Ohmin lain avulla, kun tiedetään (virta)piirin kokonaisvastus. Tässä tapauksessa virta kiertää kummankin vastuksen läpi, ja sanotaan, että vastukset ovat sarjassa. Piirin kokonaisvastus on tällöin yksittäisten vastusarvojen summa. Piirin virralle saadaan:

I = E/(R_s + R).

Sijoittamalla arvot saadaan piirin virta ratkaistua:

I = 3.0V/(0.15 + 10) = n. 0.2956 A = 295.6 mA.

Nyt yksittäisten vastusten jännitteiden ratkaisu onnistuu Ohmin lain avulla, eli

U_Rs = IR_s = 0.2956 A x 0.15 = n. 0.0443 V = 44.3 mV

 ja

U_R = IR = 0.2956 A x 10 = n. 2.956 V